So you may call
In this case, there is no need for calling ll_encode. The second argument is converted implicitly to BooleSet.
Note, that {x + c} is a reduced Boolean Gröbner basis: Equivalently
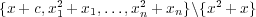
is a reduced Gröbner basis).
The goal of this section is to explain how to get most performance out of PolyBoRi using the underlying ZDD structure. This awareness can be seen on several levels
PolyBoRi is implemented as layer over a decision diagram library (CUDD at the moment).
In CUDD every diagram node is unique: If two diagrams have the same structure, they are in fact identical (same position in memory). Another observation is, that CUDD tries to build a functional style API in the C programming language. This means, that no data is manipulated, only new nodes are created. Functional programming is a priori very suited for caching and multithreading (at the moment however threading is not possible in PolyBoRi). The ite-operator is the most central function in CUDD. It takes two nodes/diagrams t, e and an index i and creates a diagram with root variable i and then-branch t, else-branch e. It is necessary that the branches have root variables with bigger index (or are constant). It creates either exactly one node, or retrieves the correct node from the cache. Function calls which come essentially down to a single ite call are very cheap.
For example taking the product x1 ⋆ (x2 ⋆ (x3 ⋆ (x4 ⋆ x5))) is much cheaper than ((((x1 ⋆ x2) ⋆ x3) ⋆ x4) ⋆ x5).
In the first case, in each step a single node is prepended to the diagram, while in the second case, a completely new diagram is created. The same argument would apply for the addition of these variables. This example shows, that having a little bit background about the data structure, it is often possible to write code, that looks as well algebraic as provides good performance.
Often there is an alternative description in terms of set operations for algebraic operations, which is much faster.
An example for this behaviour is the calculation of power sets (sets of monomials/polynomials containing each term in the specified variables). The following code constructs such a power set very inefficiently for the first three variables:
The algorithm has of course exponential complexity in the number of variables. The resulting ZDD however has only as many nodes as variables. In fact it can be constructed directly using the following function (from specialsets.py).
Note, that we switched from polynomials to Boolean sets. We inverse the order of variable indices for iteration to make the computation compatible with the principles in 2.1 (simple ite operators instead of complex operations in each step).
The following function constructs the complete homogeneous polynomial/BooleSet containing all possible monomials of degree d.
We use the set of all monomials of one degree lower using the cartesian product with the set of variables and remove every term, where the degree did not increase (boolean multiplication: x2 = x).
Sometimes, it is possible to construct the decision diagram directly, as it is theoretically known, how it looks like. In the following, we construct the same polynomial as in 2.2.2 directly by elementary if_then_else operations. This will save much recursion overhead.
In the following we will show five variants to implement a function, that computes the sum of all terms of degree d in a polynomial f.
This solution is obvious, but quite slow.
We leave it to the heuristic of the add_up_polynomials function how to add up the monomials. For example a divide and conquer strategy is quite good here.
This solution build on the fast intersection algorithm and decomposes the task in just two set operations, which is very good.
However it can be quite inefficient, when f has many variables. This can increase the number of steps in the intersection algorithm (which takes with high probability the else branch of the second argument in each step).
The repeated unnecessary iteration over all variables in f (during the intersection call in the last section) can be avoided by taking just integers as second argument for the recursive algorithm (in the last section this was intersection).
Recursive implementations are very compatible with our data structures, so are quite fast. However this implementation does not use any caching techniques. CUDD recursive caching requires functions to have one, two or three parameters, which are of ZDD structure (so no integers). Of course we can encode the degree d by the d-th Variable in the Polynomial ring.
The C++ implementation of the functionality in PolyBoRi is given in this section, which is recursive and uses caching techniques.
The encoding of integers for the degree as variable is done implicitly by our cache lookup functions.
Given a Boolean polynomial f, a variable x and a constant c, we want to plug in the constant c for the variable x.
Naive approach The following code shows how to tackle the problem, by manipulating individual terms. While this is a very direct approach, it is quite slow. The method reducible_by gives a test for divisibility.
Solution 1: Set operations In fact, the problem can be tackled quite efficiently using set operations.
Solution 2: Linear Lexicographical Lead rewriting systems On the other hand, this linear rewriting forms a rewriting problem and can be solved by calculating a normal form against a Gröbner basis. In this case the system is {x + c}∪{x21 + x1,…,x2n + xn} (we assume that x = xi for some i). For this special case, that all Boolean polynomials have pairwise different linear leading terms w. r. t. lexicographical ordering, there exist special functions. First, we encode the system {x + c} into one diagram
This is a special format representing a set of such polynomials in one diagram, which is used by several procedures in PolyBoRi. Then we may reduce f by this rewriting system
This can be simplified in our special case in two ways.
So you may call
In this case, there is no need for calling ll_encode. The second argument is converted implicitly to BooleSet.
Note, that {x + c} is a reduced Boolean Gröbner basis: Equivalently
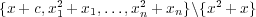
is a reduced Gröbner basis).
We want to a polynomial f(x1,…,xn) by xi ci, where c1,…,cn are constants.
ci, where c1,…,cn are constants.
Naive approach First, we show it in a naive way, similar to the first solution above.
Solution 1: n set operations The following approach is faster, as it does not involve individual terms, but set operations
For example, the call
results in 1.
We deal here with navigators, which is dangerous, because they do not increase the internal reference count on the represented polynomial substructure. So, one has to ensure, that f is still valid, as long as we use a navigator on f. But it will show its value on optimized code (e. g. PyRex), where it causes less overhead. A second point, why it is desirable to use navigators is, that their then_branch- and else_branch-methods immediately return (without further calculations) the results of the subset0 and subset1-functions, when the latter are called together with the top variable of the diagram f. In this example, this is the crucial point in terms of performance. But, since we already call the polynomial construction on the branches, reference counting of the corresponding subpolynomials is done anyway.
This is quite fast, but suboptimal, because only the inner functions (additions) use caching. Furthermore, it contradicts the usual ZDD recursion and generates complex intermediate results.
Solution 2: Linear Lexicographical Lead rewriting systems The same problem can also be tackled by the linear-lead routines. In the case, when all variables are substituted by constants, all intermediate results (generated during ll_red_nf_redsb/ll_red_nf_noredsb) are constant. In general, we consider the overhead of generating the encoding d as small, since it consists of very few, tiny ZDD operations only (and some Python overhead in the quite general ll_encode).
Since the tails of the polynomials in the rewriting system consist of constants only, this forms also a reduced Gröbner basis. Therefore, you may just call
This is assumed to be the fastest way.
We used ll_red_nf_redsb/ll_red_nf_noredsb functions on rewriting systems, where the tails of the polynomials was constant and the leading term linear. They can be used in a more general setting (which allows to eliminate auxiliary variable).
Definition 2 Let L be a list of Boolean polynomials. If all elements p of L have pairwise different leading terms with respect to lexicographical ordering, then we call L a linear lexicographical lead rewriting system.
We know that such a system forms together with the complete set of field equations a Gröbner basis w. r. t. lexicographical ordering.
In particular we can use ll_red_nf_redsb to speedup substitution of a variable x by a value v also in the more general case, that the lexicographical leading term of x + v is equal to x. This can be tested most efficiently by the expression
In many cases, we have a bigger equation system, where many variables have a linear leading term w. r. t. lexicographical ordering (at least one can optimize the formulation of the equations to fulfill these condition). These systems can be handled by the function eliminate in the module polybori.ll. I returns three results: